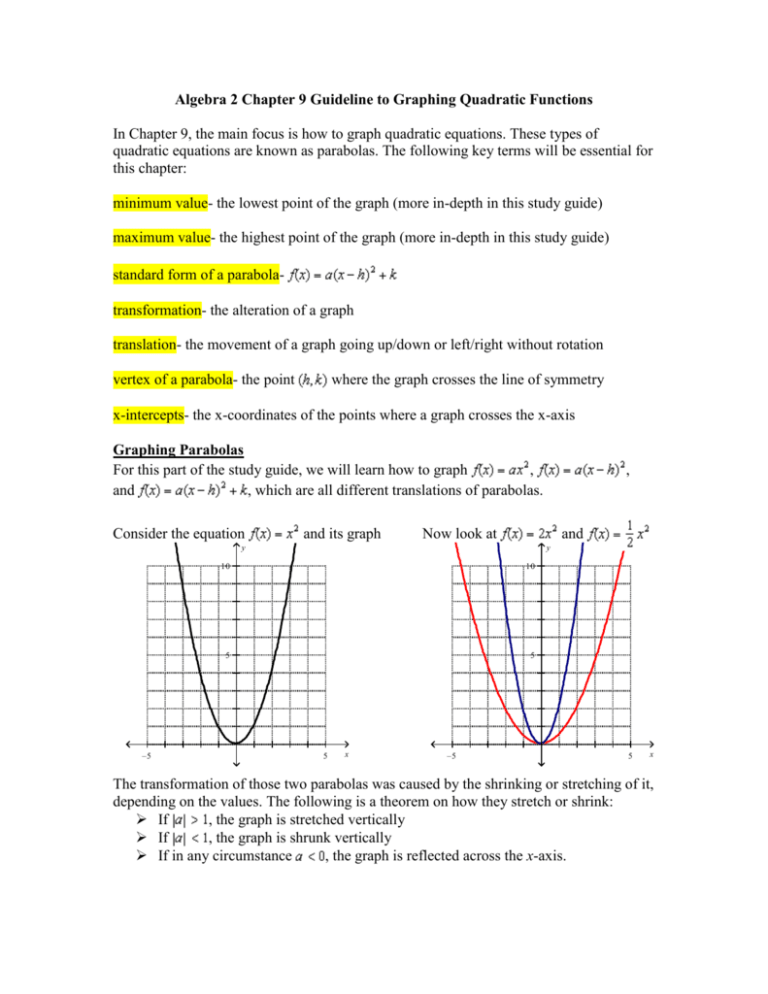
In order for us to have a vector space, we will need, for example, to think of $3x$ as a quadratic function. Whether or not we have a vector space depends on how you interpret "quadratic function whose graph passes through the origin." One, how does passing through the origin affect the supposed vector space - my assumption is that it affects axiom one? And two, how would the vectors be described?
I specifically have two questions in addition to proving the vector space. The exact problem: prove that the set of all quadratic functions whose graphs pass through the origin with standard operations is a vector space. The idea is to prove that this is a vector space based upon the following axioms:
0 kommentar(er)
